関連クイズ
-

確率の問題
確率の問題です。難易度は高校入試レベルから大学入試レベルまで様々です。…
難易度 問題数 全20問
問題数 全20問
-

平成24年度埼玉県公立高校入試問題 改
埼玉県の高校入試史上最高難度の問題です。中学生レベルで考えてください。全体の平均点が、36.5点でした。…
難易度 問題数 全5問
問題数 全5問

クイズの答え
Q.1
出題文: A点からB点まで最短距離を移動するときに、P点を通る確率は?
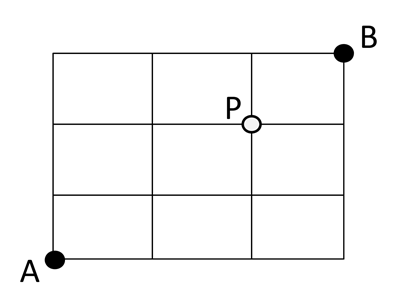
こたえ: 3/5
Q.2
出題文: 白い碁石が3個、黒い碁石が2個ある。この5つの碁石を、例のように左から順に並べた時、両端に白い碁石が並ぶ確率は?
こたえ: 3/10
解説: ?????と順番に番号をふる。2つの黒い碁石が何番目に来るか考えると、並び方は全部で 5×4÷2=10通りある。 このうち、両端に白い碁石が来る並び方は、2つの黒い碁石が???のうちの2つに来る時だから、3×2÷2=3通り。 よって、両端に白い碁石が並確率は10分の3。
Q.3
出題文: TOKYOという5文字を並べ替えた時、OOが並ぶ文字列になる確率は?
こたえ: 2/5
解説: 5文字を並べると5×4×3×2×1通りの並べ方があるが、Oが2個あるため、すべての並べ方は(5×4×3×2×1)÷2通りになる。 OとOが並ぶとき、OOを一文字としてPに置き換え計算すれば、TKYPの4文字の全部の並べ方は、(4×3×2×1)通りになる。 よって、TOKYOという5文字を並べ替えた時、OOが並ぶ文字列になる確率は、(4×3×2×1)÷[(5×4×3×2×1)÷2]=2/5になる。
Q.4
出題文: A君、B君、C君の3人がジャンケンをして順位を決めます。3人のうち1位が決まった場合、または3位が決まった場合は、つぎのジャンケンには参加しません。この時、2回目のジャンケンで3人の順位がすべて決まる確率は?ただし、グー、チョキ、パーを出す確率は、3人とも同じとする。
こたえ: 4/9
解説: 1回目のジャンケンでA君、B君、C君のグー、チョキ、パーの出し方は全部で3×3×3=27通り。このうち1人が勝ち、2人が負けるのは3×3=9通り。1人が負け、2人が勝つのも3×3=9通り。よって、1回目のジャンケンで誰かが1位または3位に確定する確率は(9+9)÷27=2/3。 1回目のジャンケンで誰かが1位または3位に確定した場合、残る2人のグー、チョキ、パーの出し方は全部で3×3=9通り。このうち、2人が引き分けるのは2人ともグー、チョキ、パーのうち同じものを出す場合だから、全部で3通り。よって、2回目のジャンケンで2人の順位が決まる確率は、1−3/9=2/3。 よって、2回目のジャンケンで3人の順位がすべて決まる確率は2/3×2/3=4/9。
Q.5
出題文: 箱の中に白い球が4個、赤い球が5個、青い球が3個入っています。Aさんが、続けて3個の玉を箱から取り出した時に、3個とも赤い球である確率は?
こたえ: 1/22
解説: はじめに赤い球を取る確率は5/12。次に赤い球を取る確率は4/11。3番目に赤い球を取る確率は3/10。よって、3個の玉がいずれも赤い球になる確率は5/12×4/11×3/10= 1/22。

確率の問題です。難易度は高校入試レベルから大学入試レベルまで様々です。…
難易度 問題数 全20問
問題数 全20問

埼玉県の高校入試史上最高難度の問題です。中学生レベルで考えてください。全体の平均点が、36.5点でした。…
難易度 問題数 全5問
問題数 全5問